Chaque jeu définit un monde. Au même titre que les lois de la physique régissent le nôtre, un jeu est régi par ses règles. De l'assemblage de ces règles émergent des propriétés qui font la richesse du jeu.
L'informatique nous permet d'explorer en profondeur les propriétés d'un jeu en simulant un grand nombre de parties (simulation dite de Monte-Carlo). L'on voit ansi émerger un certain nombre de propriété.
Par exemple, nous avons exploré dans un article précédent les propriétés liées à un jeu de lancer de dés faisant partie de Risk1. Le jeu de la vie n'est pas à proprement parler un jeu à plusieurs joueurs, mais les règles qui le définissent font aussi apparaître des propriétés émergentes2, étonnantes à mon opinion.
La bataille corse est un jeu de cartes. Contrairement à la bataille ou seul le hasard de la distribution initiale conditionne la victoire, pour gagner à la bataille corse ce sont les réflexes, la concentration, et la mémoire qui comptent pour gagner.
Nous présentons dans ce document certaines propriétés émergentes de la bataille corse.
Règles du jeu
C'est un jeu qui comporte de nombreuses variantes articulées autour d'un noyau commun. Voici les règles codées dans le simulateur.
-
La partie est jouée à deux joueurs seulement.
-
La partie se joue avec un jeu de 52 cartes classique.
-
Chaque joueur joue avec un jeu identique (2 as, 2 rois, 2 dames, 2 valets, 18 faibles).
-
L'ordre du jeu est différent pour chaque joueur et est choisi aléatoirement.
-
Le premier à jouer est choisi aléatoirement par le simulateur.
-
Le perdant est le joueur qui pose sa dernière carte.
-
Chaque joueur est caractérisé par sa probabilité de taper notée ci dessous p_taper (joueur A: p, joueur B: 1-p, 0<=p<=1).
-
Chaque joueur joue tour à tour.
-
On tape quand deux cartes identiques se suivent sur le tas central.
-
Toutes les paires sont tapées (y compris les paires d'atout).
-
Le tour d'un joueur consiste à déposer un certain nombre de cartes sur le tas central (1,2,3 ou 4).
-
Un joueur ramasse le tas central quand il a tapé une paire le premier ou qu'il a déposé un atout (as,roi,dame,valet) victorieux.
-
Un atout est victorieux quand le joueur adverse le recouvre d'un nombre N de cartes faibles (1 pour un valet, 2 pour une dame, 3 pour un roi, 4 pour un as).
-
Quand un joueur recouvre un atout X par un autre atout Y avant la fin du décompte des cartes (1 pour un valet, 2 pour une dame, 3 pour un roi, 4 pour un as), la situation s'inverse et c'est à l'autre de joueur de jouer N cartes, dépendamment de l'atout Y.
Propriétés émergentes
Protocole experimental
Les règles codées dans le simulateur (section précédente) réduisent l'aléatoire et fixent le maximum de paramètres (e.g., avoir le même jeu au début). Pour chaque propriété étudiée, l'étude se fait après:
-
N parties simulées, dans le cas d'une propriété sans variable libre e.g. la propriété A
-
M*K parties simulées dans le cas d'une propriété à 1 variable libre e.g. la propriété B
Notons que N et M sont du même ordre de grandeur, plus ils sont grands plus les résultats sont précis (mais aussi plus l'obtention des résultats est long). Un bon compromis empirique a fixé N~=300. N et M sont notés essai dans les graphiques ci dessous. La valeur de K peut être fixe dans la cas où la variable libre est sur une echelle nominale. Dans le cas d'une echelle intervalle, la valeur de K fixe le degré de continuité de la courbe obtenue. Plus K est grand, plus la courbe est lisse.
Propriété A: Histogramme de la durée de la partie pour une probabilité de taper identique (p_taper=0.5)
La propriété A concerne la durée de la partie quand les deux joueurs sont de niveau égal, c'est à dire qu'ils ont la même probabilité de taper pour remporter un pli.
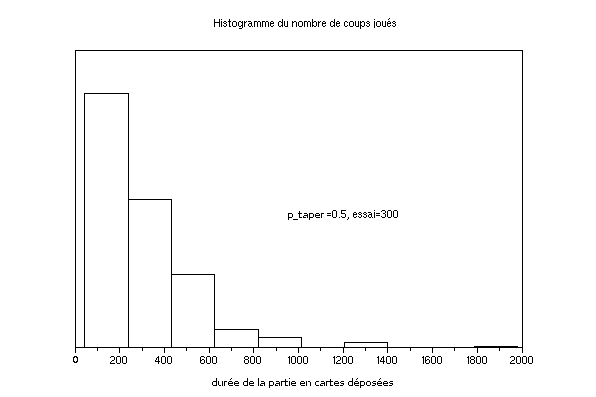
Cet histogramme nous montre que la durée des parties est très variable, d'un facteur 1 à 6 pour la grande majorité des parties (entre 100 et 600 coups joués), et pouvant monter jusqu'à presque 2000 coups !
Propriété B: L'influence de la probabilité de taper sur la durée du jeu
La propriété B concerne l'influence de la probabilité de taper sur la durée médiane du jeu exprimée en nombre de cartes déposées.
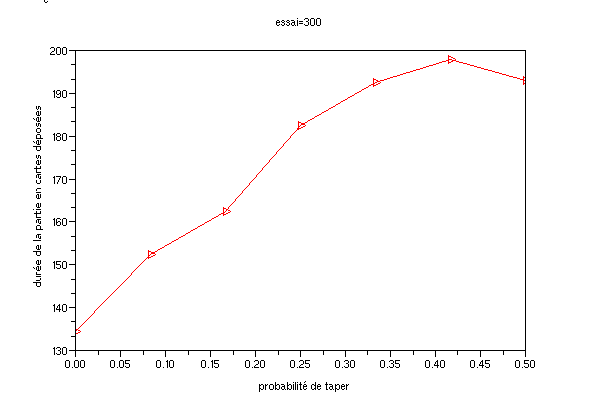
La probabilité de taper (p_taper) a une influence sur la durée médiane de la partie. Ce n'est pas surprenant. En effet, quand un joueur est moins bon que son adversaire, c'est à dire qu'il tape moins souvent, l'adversaire gagne plus vite. Notons toutefois que la variation de la durée médiane de la partie est assez faible (~50%) de 135 à 190 coups environ. Je ne saurais dire si la légère decroissance vers p_taper=0.5 est accidentelle (due à la simulation Monte-Carlo) ou non. J'ai vu apparaître ce phénomène sur un grand nombre de courbes générées. Pourtant, je ne vois pas d'explication pour qu'une partie dure plus longtemps quand il y a un léger désavantage entre les deux adversaires.
Propriété C: L'influence de la probabilité de taper sur la probabilité de gagner
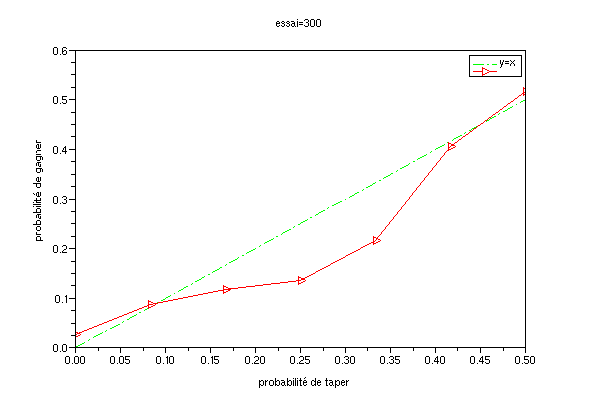
Cette courbe est très intéressante. On y constate tout d'abord que la probabilité de gagner n'est pas égale à la probabilité de taper. Le hasard de la distribution initiale conduit à des parties ou un joueur qui ne tape jamais (p_taper ~ 0) peut quand même gagner. Pour p_taper autour de 0.3, le jeu est relativement inégal, c'est à dire que la probabilité de gagner est bien inférieure à la probabilité de taper. C'est le fameux sentiment d'injustice de la bataille corse: pourquoi mon adversaire gagne-t-il si souvent alors que je tape quand même souvent ? La situation se rétablit pour p_taper environ égale à 0.4.
Propriété D: La force comparée des atouts
La propriété D essaie de quantifier la force des atouts (as, roi, dame et valet). Une analyse qualitative simple des règles montre que le valet est la plus forte des cartes, suivi de la dame, du roi, et enfin de l'as. Mais dans quelle mesure ? La figure suivante nous le montre. Pour obtenir ces valeurs, le protocole expérimental est de donner un jeu identique au deux joueurs, à l'exception d'une à quatre cartes (ex: 4 as / 4 rois / 4 dames/ 0 valets / 20 faibles contre 4/4/4/4/16) et de l'ordre du jeu . Bien entendu, les deux joueurs ont la même probabilité de taper.
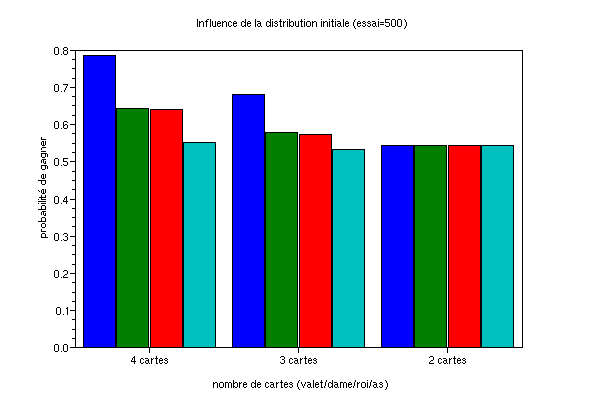
Notez bien que ce graphique est le résultat d'une simulation Monte Carlo, et qu'en conséquence les faibles écarts ne sont pas significatifs. Ce graphique confirme l'intuition que le valet est la carte la plus forte. Nous apprenons deux autres choses:
-
le valet est une carte très puissante: la probabilité de gagner en ayant les 4 valets au départ est de l'ordre de 80%
-
la différence de puissance entre les atouts restants (dame,roi,as) est beaucoup plus faible (voire non significative). Contrairement à l'intuition, ce graphique nous montre qu'avoir 3 dames vaut à peine mieux qu'avoir 3 as !
Propriété E: Influence de la variante sandwich sur la propriété B (durée)
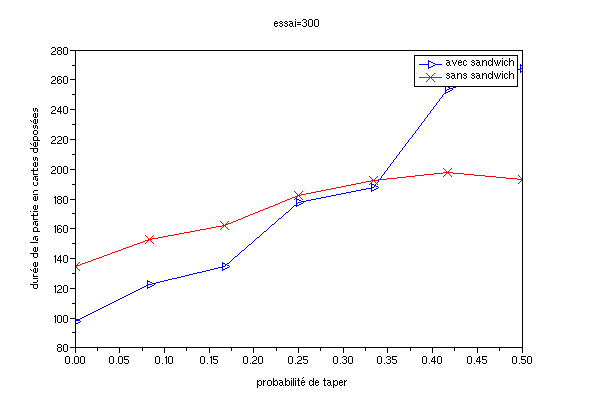
La variante sandwich de la bataille corse consiste à taper les paires séparées par une autre carte (métaphore du sandwich); par exemple un 2, un valet, un 2. Cette variante restreint l'influence du hasard car on tape plus souvent. Logiquement, les parties durent moins longtemps quand la différence de niveau entre les joueurs est grande. Par contre les parties durent plus longtemps quand les joueurs sont de niveau équivalent.
Propriété F: Influence de la variante sandwich sur la propriété C (victoire)
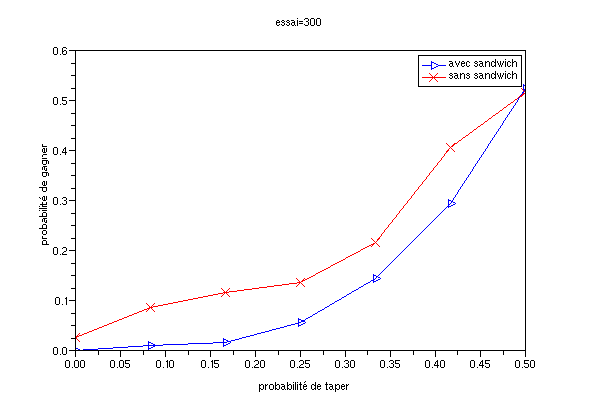
La variante sandwich influe non seulement sur la durée du jeu, mais aussi sur son type. La courbe bleue p_gagner=f(p_taper) est bien en dessous de la courbe rouge. De plus elle tend vers 0. La variante sandwich fait donc quasiment disparaître le hasard du jeu, et ne permet plus à un joueur qui ne tape jamais de gagner une seule partie. Elle creuse aussi les écarts de niveaux. Avec cette variante, on a beau taper 3 fois sur 10, on ne gagne plus que 1 fois sur dix !
De plus, regardons les pentes de la courbe bleue. Elle sont très faible au début, et très forte à la fin. Cela a deux conséquence sur l'apprentissage à la bataille corse:
-
pour des joueurs avec un grand écart de niveau, le moins bon aura beau progresser pour taper, il gagnera toujours peu (et surtout pas beaucoup plus) de parties (pente faible vers p=0).
-
inversement, pour des joueurs de niveaux différents, mais proches, si le moins bon progresse un tout petit peu (i.e., tape plus vite), il gagnera tout de suite beaucoup plus de parties (pente forte vers p=0.5).
Conclusion
Nous avons présenté quelques propriétés émergentes de la bataille corse obtenues par simulation Monte-Carlo. Nous pensons que les propriétés C et F sont les plus intéressantes. D'une part elles caractérisent le type du jeu (jouabilité, apprentissage), d'autre part elles montrent qu'une variante simple peut considérablement changer le jeu. Ceci amène un problème général de théorie des jeux (plus au sens socio-cognitif que mathématique). Soit la famille des jeux à 2 joueurs où intervient une probabilité p/1-p (quels jeux appartiennent à cette famille ?) la courbe de la propriété C est une sorte de signature pour chaque jeu de cette famille. Quelle est la courbe rendant le jeu le plus agréable (sous quelles hypothèses sociales, cognitives, etc.) ?
Martin Monperrus (2007) - Toutes les remarques et questions sont les bienvenues.
2par exemple, Quelques propriétés remarquables du jeu de la vie